Homepage von Stefan Strömsdörfer

    Die dunkle Seite (Rätsel, Illusionen, Basteleien...)
 

Warum "die dunkle Seite"?
Zum einen wegen dem anderen Hintergrundbild, hauptsächlich aber wegen der vielen sinnlosen Aktivitäten von mir, die mir wenig bringen, aber trotzdem viel Zeit in Anspruch nehmen.

Ich kann hier leider nur eine sehr kleine Auswahl von Spielereien, die ich so betreibe und betrieben habe, auflisten. Das liegt u.a. am Platz, aber ich kann mich einfach nicht mehr an all den Mist erinnern, der mir während meines Lebens so eingefallen ist.

Zu den Illusionen gebe ich keine Erklärungen an, da ich womöglich noch irgendetwas falsches schreibe, wenn ich versuche, alles haargenau zu erklären. Ich denke man sollte sich darüber selber ein bißchen den Kopf zerbrechen (zur Not tut's auch eine mail, dann kann ich ja immer noch einen Erklärungsversuch starten).

Die Rätsel sind, wenn nicht anders gekennzeichnet, Denksportaufgaben (=Logikaufgaben). Es sind keine Probier-aufgaben (z.B. magische Quadrate) oder dumme Rechnereien (z.B: ich bin doppelt so alt wie die Quersumme des Alters von ... hoch der x-ten zahl des Alters von ... usw.).

Aber nun zu den essentiellen Dingen eines glücklichen Lebens: 

•  Geometrische Illusionen

• Optische Täuschungen

• Denksportaufgaben

• Basteln von geometrischen Körpern

• Witze über Mathematiker/Physiker/Ingenieure

Geomtrische_Illusionen

Dieses kleine Problem sollte eigentlich jeder kennen, der sich mit optischen Täuschungen und Illusionen beschäftigt. Mir gefällt es trotzdem immer wieder und es macht immer wieder Spaß, es neu zu entwickeln (zeichnen), wenn man die genaue Struktur vergessen hat.
 
 





schiefes Quadrat

Das gleiche Prinzip wie beim Dreieck. Das Ganze läßt sich natürlich auf n-Ecke erweitern, ist dann aber nur noch langweilige Beschäftigungstherapie.



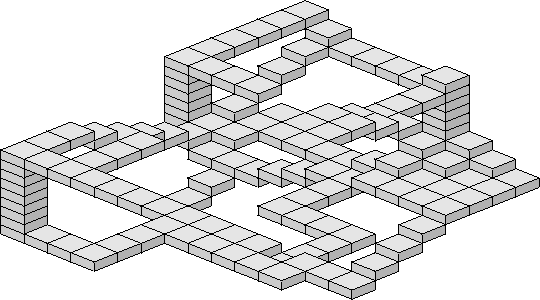
endlose Treppen

Eine meiner Leblingsillusionen, weil man damit beliebig komplizierte Figuren mit einer sehr großen Ausdehnung erstellen kann. Vor allem sehen die Treppen immer wieder anders aus. Das Ganze ist zwar nicht so professionell wie das endlos fließende Wasser von M.C.Escher, aber durchaus verwirrend genug, wenn man versucht, die Treppen gedanklich entlangzulaufen und dabei die "Stockwerke" mitzählt.

Hier noch eine andere, ziemlich bekannte Illusion:



-> Themenübersicht

Optische_Täuschungen

krumme Linien?

Auch ziemlich bekannt, aber immer wieder nett anzusehen. Am Bildschirm wird durch die Pixel sofort klar, dass die zwei horizontalen Linien wirklich gerade sind. Ein interessantes Experiment dazu: wenn man zuerst die zentralen Linien (mit Bleistift) zieht und dann ohne Lineal zwei gerade Linien (mit Kugelschreiber), danach die Bleistiftlinien wegradiert, wundert man sich, dass man trotz Vorwissens die Linien krumm zeichnet (zumindest wenn man das Ganze richtig anstellt). Es gibt noch viele Täuschungen, die sich aus dieser ableiten lassen, aber ich denke, dieser 'Prototyp' ist eindrucksvoll genug.
 
 





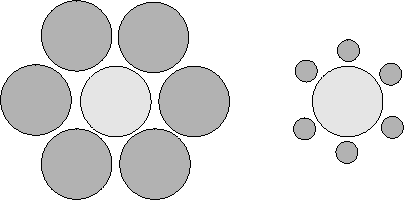
kleiner und großer Kreis?

Wer's nicht glaubt, kann die Durchmesser der hellen (inneren) Kreise nachmessen: auf's Pixel genau gleich groß!

Hier noch eine kleine Sammlung von anderen Optischen Täuschungen:

die waagrechten Linien sind wirklich waagrecht !	die schrägen Linien sind parallel
die dunklen Schatten sind eine Illusion	die Linie links ist "gerade", rechts ist die untere Linie die Fortsetzung der linken
keine Spiralen, sondern Kreise !	die zwei Objekte sind gleich groß !
das ist ein Kreis !

-> Themenübersicht

Denksportaufgaben

I) Schlitten (Physik-Aufgabe)
Angenommen, eine Person zieht einen Schlitten mit einer konstanten Geschwindigkeit von 0,5 m/s. Währenddessen fallen 0,1 kg/sec Schnee (senkrecht) auf den Schlitten. Wenn man Gleitreibung, Luftwiderstand etc. vernachlässigt, welche Kraft F muss die Person aufwenden, um den Schlitten mit konstanter Geschwindigkeit zu ziehen? Dazu gibt es zwei Ansätze:
a) Energieerhaltung:
Die kinetische Energie des Schlittens erhöht sich pro Sekunde um ½Dmv²=½*(0,1kg)*(0,5²gm²/s²)=0,0125 Nm, das entspricht einer Leistung von 0,0125 Watt. Das ist gleich der verrichteten Arbeit/Zeit der Kraft F: W=F*Ds/t=F*Dv=F*(0,5m/s). Also ist (F=0,0125Nm/s)/(0,5m/s)=0,025 N.
b) Impulserhaltung:
Der Impuls des Schlittens erhöht sich um Dmv oder (0,1kg)*(0,5m/s)=0,05kgm/s. Das ist gleich der Kraft F mal Zeit(1s). Also ist F=(0,05kgm/s)/s=0,05kgm/s²=0,05N.
Welche Antwort stimmt und wo steckt der Fehler???
( Falls jemand Probleme mit der Darstellung hat: "D" ist ein "Delta"! )
Lösung

II) Schnürsenkel
Du bist in einem Raum eingesperrt und hast nur zwei Schnürsenkel und ein Feuerzeug. Alles, was Du weisst ist, dass jeder Schnürsenkel genau eine Stunde braucht, um ganz abzubrennen. Du weisst aber auch, dass die Schnürsenkel nicht gleichmäßig abbrennen. Jetzt Deine Aufgabe: Du sollst mit den verfügbaren Mitteln genau 45 Minuten „abmessen“.
Lösung
III) Lichtschalter
Du stehst vor einem Raum, in dem eine Glühlampe hängt. Vor der Tür sind drei Lichtschalter, von denen alle die Lampe schalten, aber zwei davon sind kaputt. Die Schalter sind anfangs alle auf „aus“-Stellung. Du darfst nun die Schalter sooft/solange Du willst betätigen und anschließend einmal(!) den Raum betreten. Danach musst Du wissen, welcher Schalter funktioniert!
Lösung
IV) Kisten, Schlösser, Schlüssel und die Münze
Du und Dein Freund stehen auf verschiedenen Seiten eines Flusses, der von einem diebischen Fährmann besetzt ist. Jeder von euch (Du und Dein Freund) haben jeweils eine Kiste, ein Vorhängeschloss und einen genau für das Schloss passenden Sclüssel. Du hast außerdem eine Münze, die Du Deinem Freund schenken willst. Du kannst Gegenstände nur mit Hilfe des diebischen Fährmanns über den Fluss transportieren. Der klaut alles außer eine abgeschlossene Kiste! Bringe nun die Münze zu Deinem Freund, indem der Fährmann maximal dreimal über den Fluss fahren muss.
Lösung
V) Goldbarren
Ein König hat zehn Stapel Goldbarren mit jeweils zehn Goldbarren zu je einem Kilogramm. Eines Tages kommt ein Dieb und schabt in einem Stapel von jedem Barren 10 Gramm Gold ab. Der König hat eine sehr genaue Waage, die beliebig viel Gewicht wägen kann. Er wiegt jeden Tag seine Goldbarren auf eine bestimmte Weise. Er benutzt dabei genau eine(!) Wägung und erkennt sofort, von welchem Stapel Gold fehlt. Wie macht er das?
Lösung
VI) 13 Münzen
Du hast 13 Münzen, von denen eine falsch ist. Du weisst aber nur, dass die falsche ein anderes Gewicht hat, aber nicht, ob die Falsche schwerer oder leichter ist als die richtigen. Du musst nun auf einer Balkenwaage mit nur drei Wägungen die falsche Münze herausfinden!
Lösung
VII) 12 Münzen
Alles wie bei VI), jedoch nur mit 12 Münzen und Du musst herausfinden, ob die falsche Münze leichter oder schwerer ist!
Lösung
VIII) 12 Hennen
Wenn 2 Hennen 2 Tage brauchen, um 2 Eier zu legen, wie lange brauchen dann 12 Hennen, um 12 Eier zu legen?
Lösung
IX) Monate (Scherzfrage)
Wieviele Monate haben 28 Tage?
Lösung
X) Äpfel (Scherzfrage)
Wieviele Äpfel hast Du, wenn Du 2 von 3 Äpfeln wegnimmst?
Lösung
XI) Wasser (Scherzfrage)
"Fällt" ein Stück Eisen durch 40° Fahrenheit warmes Wasser schneller als durch 20° Fahrenheit warmes?
Lösung
 
XII) 2 Kobolde
Du kommst an eine Weggabelung, an der zwei Kobolde stehen. Einer von beiden lügt immer, der andere sagt immer die Wahrheit. Einer der beiden Wege führt zu einem Schatz, der andere ist von Wegelagerern übersät. Wie findest Du heraus, hinter welchem Weg der Schatz ist, wenn Du an die Kobolde nur eine Frage stellen darfst?
Lösung
XIII) Eiswasser (Physik-Aufgabe)
In einer Schüssel mit 0°C kaltem Wasser schwimmen einige Eiswürfel. Wenn die Eiswürfel schmelzen, sinkt oder steigt dann der Wasserstand?
Lösung
XIV Lügner
Ein Metzger und ein Bäcker sitzen im Wirtshaus. Der rothaarige sagt:"Ich bin der Metzger" und der schwarzhaarige sagt:"Ich bin der Bäcker". Wenn mindestens einer der beiden lügt, wer ist was?
Lösung
XV 3 Münzen (Stochastik)
Auf einem Tisch liegen je ein Viertel-, ein halber und ein ganzer Dollar. Harry besitzt eine Münze und Joe die anderen zwei. Sie werfen jeder ihre Münzen hoch, und eine Münze, die mit "Wappen" nach oben auf dem Tisch liegt, zählt nichts, eine mit "Zahl" nach oben zählt ihren Wert. Wer nun insgesamt den höheren Wert hat, bekommt die Münze(n) des anderen. Welche Münze(n) muss Harry besitzen, damit das Spiel fair ist?
Lösung
XVI Brücke
In einer Nacht stehen auf einer Seite einer alten Brücke 4 Personen, die auf die andere Seite wollen. Sie haben nur eine Fackel und die Brücke kann maximal 2 Personen tragen. Wenn 2 Personen die Brücke gleichzeitig die Brücke überqueren, brauchen sie so lange wie die langsamere der beiden. Da die Brücke schon Löcher hat, muss bei einer Überquerung immer die Fackel dabeisein. Um die Brücke zu überqueren, benötigt Person A 1 Minute, Person B 2 Minuten, Person C 5 Minuten und Person D 10 Minuten. Die Personen sollen nun in 17 Minuten die Brücke überqueren.
Lösung
XVII Mühlstein
Der Mühlstein eines Müllers ist in vier Teile zerbrochen, die alle ein Gewicht in ganzen Kilogramm haben. Der Müller sagt, dass er mit diesen vier Steinen und einer Balkenwaage alle ganzzahligen Gewichte bis 50 kg bestimmen kann. Wenn der Mühlstein vorher 50 kg wog, wie schwer sind die vier Bruchstücke?
Lösung

 

-> Themenübersicht

Basteln_von_geometrischen_Körpern

Vorwort:
Ich habe die Körper in Form von sog. Netzen gezeichnet. D.h., wenn man dieses Netz ausschneidet (natürlich zuerst ausdrucken!) und die Linien innerhalb des Netzes als sog. Bergfalten knickt, erhält man, wenn man die freien Kanten zusammenklebt, den fertigen Körper.
Vorsicht: Ich habe bei den Netzen noch keine Klebeflächen vorgesehen! Deshalb entweder mit Tesafilm arbeiten oder vorsichtshalber an jeder Kante eine Klebefläche (am besten in Trapezform) stehenlassen.
Für Mathematiker/Physiker oder sonstige Interessierte:
Jeden der Platonischen und Archimedischen Körper kann man in eine Kugel einbeschreiben, d.h. die Ecken (nicht Kanten!) liegen auf der Oberfläche einer Kugel.
Jedem Platonischen Körper kann man zudem eine Kugel einbeschreiben.
Die Platonischen Körper bestehen aus einer Sorte von regelmäßigen n-Ecken, die Archimedischen aus unterschiedlichen Sorten von regelmäßigen n-Ecken.
In den von mir entwickelten Körper lässt sich weder eine Kugel ein- noch umbeschreiben!

Hier eine Übersicht inklusive 3D-Modelle!

Hier zuerst die Platonischen Körper:
 

- Tetraeder (1.2 K)
- Würfel (1.6 K)
- Oktaeder (1.7K)
- Ikosaeder (2.7 K)
- Dodekaeder (3.4 K)
Hier die Archimedischen Körper:
 
- Abgestumpftes Tetraeder (2.4 K)
- Kuboktaeder (2.6 K)
- Abgestumpftes Ikosaeder (Fußball) (9.1 K)
- Abgestumpftes Dodekaeder (9.5 K)
- Ikosidodekaeder (5.7 K)
- Abgestumpftes Ikosidodekaeder (19.2 K)
- Rhombikuboktaeder (4.1 K)
- Snub-Dodekaeder (10.7 K)
- Snub-Kubus (5.3 K)
- Abgestumpftes Kuboktaeder (7.7 K)
- Abgestumpfter Würfel (4.4 K)
- Abgestumpftes Oktaeder (4.0 K)
- Rhombikosidodekaeder (10.6 K)
Sorry, falls einige der Bezeichnungen falsch sind.

Hier ein von mir entwickelter Körper auf Tetraederbasis (5.2 K)

Hier sind endlich die nichtkonvexen Körper:
Falls es jemanden interessiert, was eigentlich ein nichtkonvexer Körper ist: Die anderen Körper sind stets nach außen gekrümmt (=konvex), d.h. es gibt keine "Täler" auf ihrer Oberfläche. Bei nichtkonvexen Körpern gibt es jedoch auch Talfalten.



5 verschachtelte Tetraeder

Dieser Körper ist der erste nichtkonvexe, den ich gebaut habe. Das größte Hindernis dabei war, die genaue Form der einzelnen Flächen auszurechnen. Dazu muss man sich über die Geometrie des Körpers im klaren werden: er besteht aus 5 ineinandergeschachtelten Tetraedern (siehe Bild), deren Ecken auf den Ecken eines Dodekaeders (siehe oben) liegen. Da jedes Tetraeder 4 Ecken hat und das Dodekaeder 20, wird keine Ecke doppelt belegt (5*4=20).Jetzt muss man natürlich zuerst die Lage der Ecken eines Dodekaeders im dreidimensionalen Raum ausrechnen. Das geht ohne große Probleme, wenn man mit dem richtigen Ansatz rangeht (bei mir war der dritte Ansatz der halbwegs machbare). Ausreichend dafür ist Schulmathematik (Sinussatz, Vektorrechnung, Geometrie...). Danach kann man sich die Kanten- und Flächengleichungen aufstellen (natürlich nur die, die zur Berechnung einer Fläche nötig sind). Daraus erhält man durch Schnittpunkte die (dreidimensionalen) Koordinaten der Eckpunkte einer Fläche, die man dann in zweidimensionale Koordinaten umrechnen kann (ich habe einfach die Seitenlängen und Zwischenwinkel ausgerechnet).
Die ganze Rechnerei habe ich nicht exakt, sondern mit dem Taschenrechner auf ca. 4 Stellen genau durchgeführt. Das ist jedoch exakt genug, da ich beim Basteln des Körpers keine Probleme bekommen habe (außerdem kann man die Flächen sowieso nur mit begrenzter Genauigkeit ausschneiden). Zum Basteln habe ich die 60 nötigen Elemente in 5 verschiedenen Farben (mit Marmor-Füllmuster) bedruckt und somit die 5 Tetraeder hervorgehoben.
Hier kann man sich eine Grafik mit Maßen anschauen. (Eigentlich gibt es noch eine zweite Version des Körpers, wenn man die Fläche spiegelt)



2 verschachtelte Tetraeder

Dieser Körper ist eigentlich nur eine Vereinfachung des vorherigen, da hier zwei Tetraeder in einen Würfel einbeschrieben sind. Er ist natürlich viel einfacher zu bauen: nur 24 gleichseitige Dreiecke ausschneiden und aneinanderkleben.Ich habe leider noch keine Möglichkeit gefunden, 3, 4 oder mehr als 5 Tetraeder so in eine Kugel einzubeschreiben, so dass benachbarte Ecken gleiche Abstände haben und der resultierende Körper aus identischen Seitenflächen besteht.

-> Themenübersicht

Witze_über_Mathematiker/Physiker/Ingenieure

Vorwort:
Die Witze sind natürlich nicht von mir, und ich weiss leider auch die Quelle(n) nicht mehr alle, deswegen gebe ich gar keine Quellen an, damit sich keiner benachteiligt fühlt. Ich hab' mir auch nicht die Mühe gemacht, sie zu übersetzen. Ich persönlich finde die Witze gut, aber jemand, der nichts mit Naturwissenschaften am Hut hat, denkt vielleicht anders. So oder so, viel Spaß...

A topologist is a man who doesn't know the difference between a coffee cup and a doughnut.

A statistician can have his head in an oven and his feet in ice, and he will say that on the average he feels fine.

"Algebraic symbols are used when you do not know what you are talking about."

Old mathematicians never die; they just lose some of their functions.

I saw the following scrawled on a math office blackboard in college:
        1 + 1 = 3, for large values of 1

lim  sqrt(8) --->  3
8->9
lim   sqrt (3) = 2
3->4

There are three kinds of people in the world; those who can count and those who can't.

A team of engineers were required to measure the height of a flag pole. They only had a measuring tape, and were getting quite frustrated trying to keep the tape along the pole.  It kept falling down, etc.A mathematician comes along, finds out their problem, and proceeds to remove the pole from the ground and measure it easily. When he leaves, one engineer says to the other:  "Just like a mathematician! We need to know the height, and he gives us the length!"

A man camped in a national park, and noticed Mr. Snake and Mrs. Snake slithering by.  "Where are all the little snakes?" he asked.  Mr. Snake replied, "We are adders, so we cannot multiply."The following year, the man returned to the same camping spot.  This time there were a whole batch of little snakes.  "I thought you said you could not multiply," he said to Mr. Snake.  "Well, the park ranger came by and built a log table, so now we can multiply by adding!"
 

If lim (8/x) = oo (infinity),  then what does lim (5/x) = ?
     x->0                                                        x->0
answer: (write 5 on it's side)

One day a farmer called up an engineer, a physicist, and a mathematican and asked them to fence of the largest possible area with the least amount of fence.  The engineer made the fence in a circle and proclaimed that he had the most efficient design.  The physicist made a long, straight line and proclaimed 'We can assume the length is infinite...' and pointed out that fencing off half of the Earth was certainly a more efficient way to do it.  The Mathematician just laughed at them.  He built a tiny fence around himself and said 'I declare myself to be on the outside.'

An engineer, a mathematician, and a computer programmer are driving down the road when the car they are in gets a flat tire.  The engineer says that they should buy a new car.  The mathematician says they should sell the old tire and buy a new one.  The computer programmer says they should drive the car around the block and see if the tire fixes itself.

Math and Alcohol don't mix, so...
PLEASE DON'T DRINK AND DERIVE

An engineer thinks that his equations are an approximation to reality.
A  physicist thinks reality is an approximation to his equations.
A  mathematician doesn't care.

Why is the number 10 afraid of seven?
                  -- because seven ate nine.

A mathematician is a person who says that, when 3 people are supposed to be in a room but 5 came out, 2 have to go in so the room gets empty...

A mathematician and a physicist agree to a psychological experiment. The mathematician is put in a chair in a large empty room and a beautiful naked woman is placed on a bed at the other end of the room. The psychologist explains, "You are to remain in your chair.  Every five minutes, I will move your chair to a position halfway between its current location and the woman on the bed."  The mathematician looks at the psychologist in disgust.  "What? I'm not going to go through this.  You know I'll never reach the bed!"  And he gets up and storms out.  The psychologist makes a note on his clipboard and ushers the physicist in.  He explains the situation, and the physicist's eyes light up and he starts drooling.  The psychologist is a bit confused. "Don't you realize that you'll never reach her?"  The physicist smiles and replied, "Of course!  But I'll get close enough for all practical purposes!"

Dean, to the physics department.  "Why do I always have to give you guys so much money, for laboratories and expensive equipment and stuff.  Why couldn't you be like the math department - all they need is money for pencils, paper and waste-paper baskets.  Or even better, like the philosophy department.  All they need are pencils and paper."

A physicist and a mathematician setting in a faculty lounge. Suddenly, the coffee machine catches on fire.  The physicist grabs a bucket and leaps towards the sink, fills the bucket with water and puts out the fire.  The second day, the same two sit in the same lounge.  Again, the coffee machine catches on fire.  This time, the mathematician stands up, gets a bucket, hands the bucket to the physicist, thus reducing the problem to a previously solved one.

A mathematician and a physicist were asked the following question:

Suppose you walked by a burning house and saw a hydrant and a hose not connected to the hydrant.  What would you do?
P: I would attach the hose to the hydrant, turn on the water, and put out the fire.
M: I would attach the hose to the hydrant, turn on the water, and put out the fire.
Then they were asked this question:
Suppose you walked by a house and saw a hose connected to a hydrant.  What would you do?
P: I would keep walking, as there is no problem to solve.
M: I would disconnect the hose from the hydrant and set the house on fire, reducing the problem to a previously solved form.

A computer scientist, mathematician, a physicist, and an engineer were travelling through Scotland when they saw a black sheep through the window of the train.
"Aha," says the engineer, "I see that Scottish sheep are black."
"Hmm," says the physicist, "You mean that some Scottish sheep are black."
"No," says the mathematician, "All we know is that there is at least one sheep in Scotland, and that at least one side of that one sheep is black!"
"Oh, no!" shouts the computer scientist, "A special case!"

A Mathematician (M) and an Engineer (E) attend a lecture by a Physicist. The topic concerns Kulza-Klein theories involving physical processes that occur in spaces with dimensions of 11, 12 and even higher.  The M is sitting, clearly enjoying the lecture, while the E is frowning and looking generally confused and puzzled.  By the end the E has a terrible headache.  At the end, the M comments about the wonderful lecture.  The E says "How do you understand this stuff?"
M: "I just visualize the process."
E: "How can you POSSIBLY visualize something that occurs in 11-dimensional space?"
M: "Easy, first visualize it in N-dimensional space, then let N go to 11."

What is "pi"?
Mathematician: Pi is the number expressing the relationship between the circumference of a circle and its diameter.
Physicist: Pi is 3.1415927 plus or minus 0.0000001
Engineer: Pi is about 3.

Tips:
A Random Walk in Science - R.L. Weber and E. Mendoza
More Random Walks In Science - R.L. Weber and E. Mendoza
In Mathematical Circles (2 volumes) - Howard Eves
Mathematical Circles Revisited - Howard Eves
Mathematical Circles Squared - Howard Eves
Fantasia Mathematica - Clifton Fadiman
The Mathematical Magpi - Clifton Fadiman
Seven Years of Manifold - Jaworski
The Best of the Journal of Irreproducible Results - George H. Scheer
Mathematics Made Difficult - Linderholm
A Stress-Analysis of a Strapless Evening Gown - Robert Baker
The Worm-Runners Digest
Knuth's April 1984 CACM article on The Space Complexity of Songs
Stolfi and ?? SIGACT article on Pessimal Algorithms and Simplexity Analysis

Hier der Algorithmus eines C-Programmierers, wenn er nachts nicht einschlafen kann:
if (!asleep) sheep++;

-> Themenübersicht

Falls jemand noch irgendwelche gute optische Täuschungen oder Illusionen oder Rätsel oder sonstige Ergänzungen zu dieser Seite kennt, immer her damit!

zurück zur Hauptseite